A while ago my friend mentioned how it would be cool to code up a ray tracer. I agreed—it did seem like a cool thing to do—and so I made one. I think the exciting thing about ray tracing is how intuitive it is. You hear about how it works, and immediately you feel like you know how to make one. In fact, it’s so intuitive that we kind of invented it before we figured out how vision actually works.
The ancient Greeks’ idea (emission theory) was that ‘eye-beams’ leave their respective eyeballs and bounce around, eventually hitting something with some color and brightness that they (somehow) then would convey back to the eye.

(Dragon helpfully placed between A and B)
Now it turns out that this is, of course, not how vision works. Thanks to modern science, we all now know that we’re in a simulation, and that our optic nerves are mere lines of code in a supercomputer which, when it finally finishes updating, will restart and end our collective existence.
But before the great reboot occurs, we all need something to occupy our time. This brings us back to videogames, 3D graphics, and ray tracing.
Just like emission theory, ray tracing (also spelled (by me – depending on which one I want to use) ray-tracing) is a way of generating graphics by simulating the light rays ‘leaving’ an eye. Despite the ancient philosophers being wrong about the underlying physics, it turns out that ray-tracing totally works as a way of generating images.
In essence, the only photons that actually matter when you see something are the ones that are going to hit your eyeball. And if you time-reverse these, they’re leaving your eyeball – bam emission theory (and ray-tracing).
One slight difference is that technically this doesn’t simulate an eyeball – it simulates a pinhole camera, which has no depth of field – but let’s ignore this.
The Goal
I want to construct the most basic nontrivial ray-tracing environment possible. I want reflections, shades, interesting shapes, but nothing too hard. My solution is to define an environment of shiny balls in a room with different shaded walls.
To be specific, our room is a 1×1×1 cube, with opposite corners on (0,0,0) and (1,1,1).
I also made the bold (easier) choice of having everything be grayscale.
The spheres will be perfectly reflective, and the walls will be perfectly absorbing.
Coding up Ray Tracing
The math behind ray tracing really is easy. If you can break your surface into triangles, then you basically take your rays, find if they intersect with your triangles, and reflect or absorb as desired.
The Math (skip if you don’t care)
A given ray starts at a position, $\vec{pos}$, and points in a direction $\vec{v}$ (we’ll take $||v||=1$). Basically, we just want to solve for how far a ray has to go before it hits the plane defined by the triangle (that’s the variable $c$ in the following): \(\vec{pos.} + c \cdot \vec{v} = \vec{z}_1 + a*(\vec{z}_2 - \vec{z}_1) + b*(\vec{z}_3 - \vec{z}_1)\)
Then to make sure our ray is actually hitting inside the triangle, we just need to check that \(a \geq 0\), \(b \geq 0\), $a+b \leq 1$. Finally, we want the ray to be moving forward (check that \(c \geq 0\)).
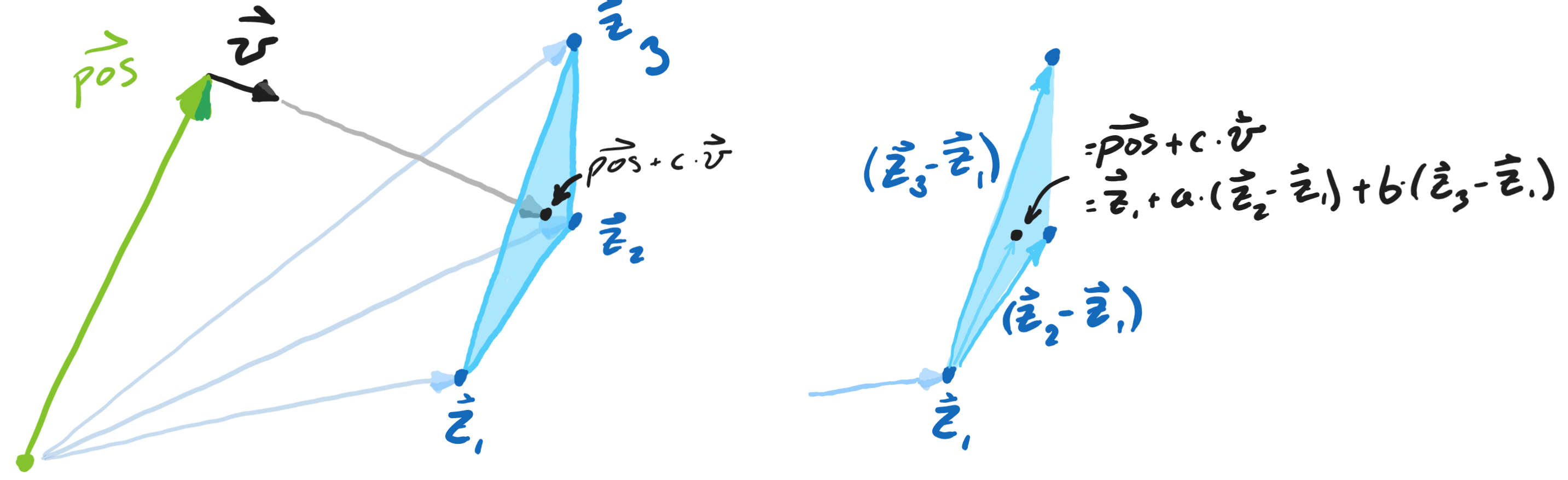
We now know where the ray is – what triangle it bumped into. Either I’ll either assign the ray the shade associated with that point on the triangle, or I’ll update $\vec{v}$ to reflect it.
Shading the Room, Shining the Balls
I don’t know what it is about these rooms I was making early on, but they were 100% cursed. Something about them was off.

We need a solution
Each wall in my room has its own shade of gray. But this alone really does not look good. Depth isn’t really conveyed well.
Humans rely heavily on shading to infer depth so let’s add some shading in here. The further away a point on the wall is from the observer, the darker its shade will be. After a little tinkering I settled on this function to make things look pretty
\[\text{shade} = \frac{\text{init_shade}}{(0.1 + \text{wall_distance}/2)^{1.2}}\]
Not only does shading make things look less haunted, we can also tell what we're looking at.
Disco Balls
This brings us to our second problem: unfortunately, it turns out that when you try to triangulate a perfectly reflective sphere, you end up with a disco ball.

Thankfully, reflecting things off a sphere might be even easier than reflecting them off a triangle. Just solve for when (if ever) the ray is a distance $r$ (the radius) from the center of a sphere, $\vec{x}$.
\[||(\vec{pos.} + c \cdot \vec{v}) - \vec{x}||^2 = r^2\]Taking \(||v|| = 1\) and writing \(\vec{x}^* = \vec{x} - \vec{pos.}\) gives us: \(c^2 - 2 c \vec{v} \cdot \vec{x}^* + (||\vec{x}^*||^2 -r^2) = 0\). Then we can solve for $c$ with the regular old quadratic formula.
Once you’ve found your solution with real and positive $c$, update the ray’s position and you’re done. To reflect, just negate the component of the ray that’s along the sphere’s radial direction.
Putting this all together, we just have to place our spheres, and start reflecting. With each reflection iteration the remaining unabsorbed light rays bounce around one more time.


There, done. Now what?
Well, we can ask ChatGPT to make sculptures for us:
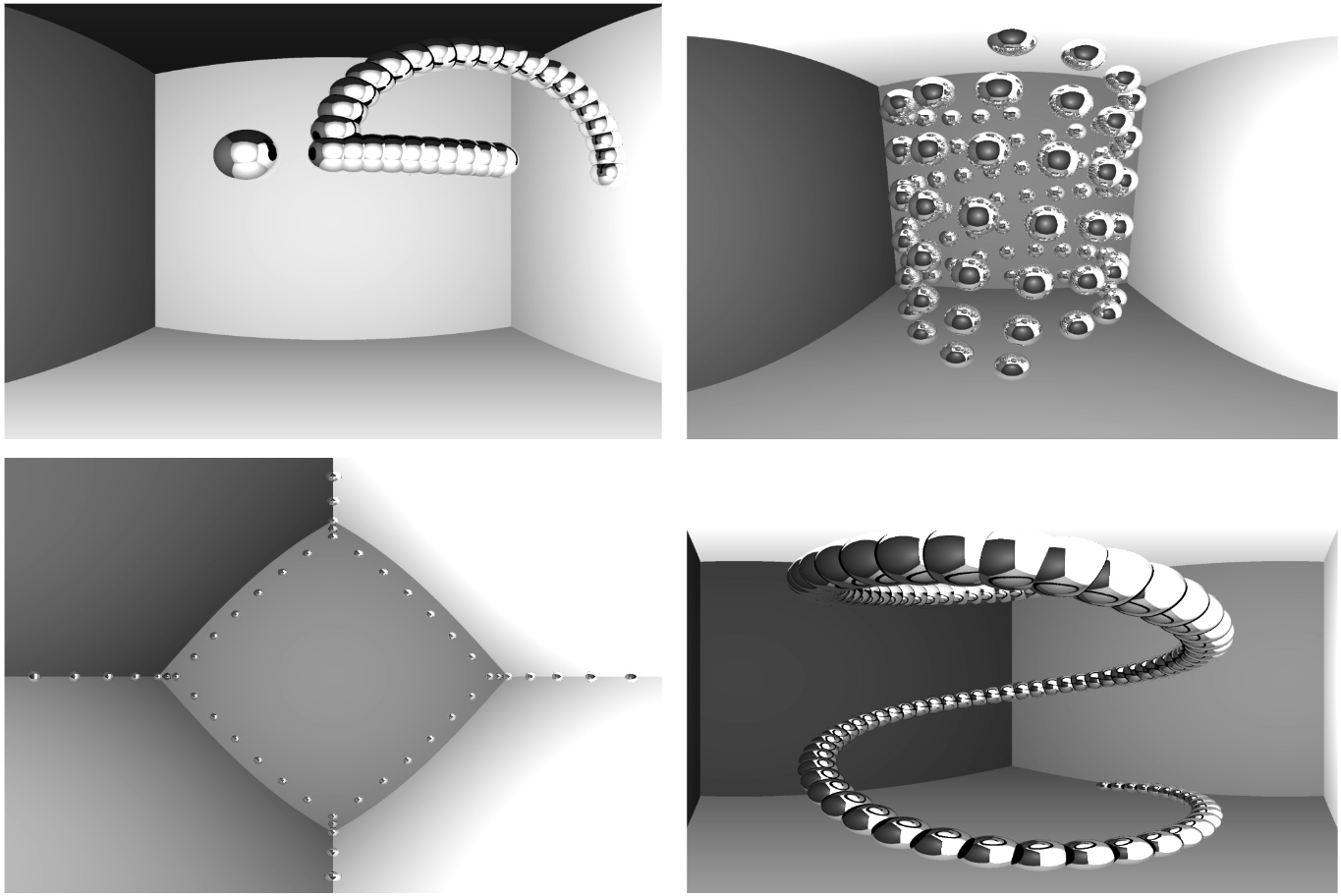
(Top left) ChatGPT's embarrassing attempt at being all deep and trying to make a question mark.
(Top right) A double helix which ChatGPT says represents the fact that it, too is made of a sort of genetic code of data.
(Bottom left) ChatGPT claimed that these tiny spheres correspond to the corners of a projected tesseract (I did not check this).
(Bottom right) A spiral, because ChatGPT seems to like spirals (they do look neat).
In Search of Fractals
But honestly I want to make something way more cool looking than these images – and what’s more cool-looking than a fractal? Nothing, that’s what. I recently learned about something called apollonian sphere packing – it’s an extension of the apollonian gasket to 3d, and this blog (which cites this other blog) described a pretty simple way to generate it.
So I coded it up and started making pretty pictures with my ray tracer:
Generation 1
At generation 1, we have 4 spheres in a tetrahedron.
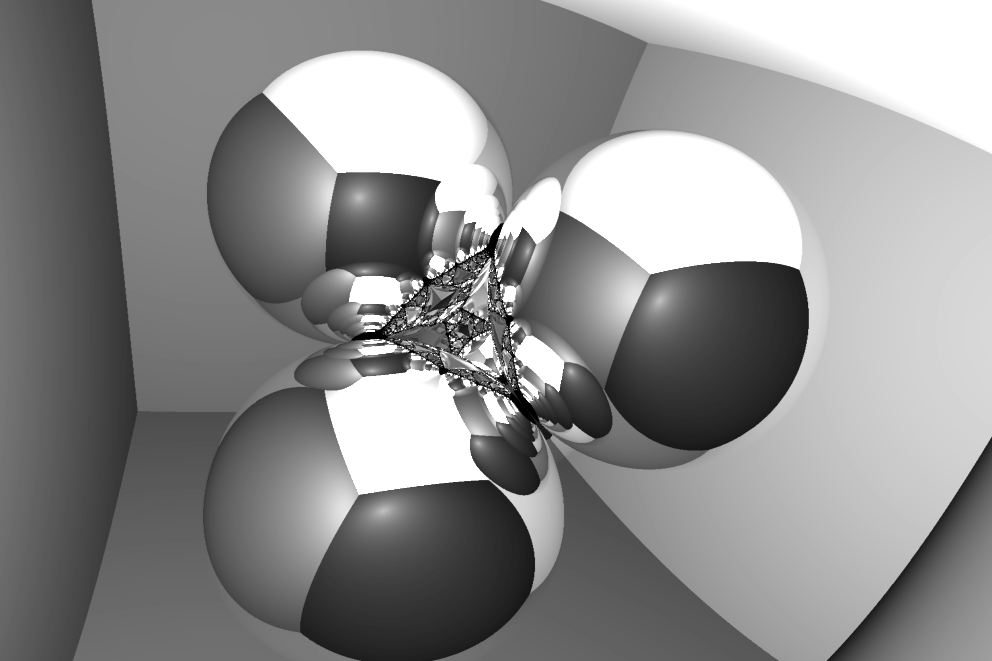
Looks pretty cool. Let’s go to generation 2
Generation 2
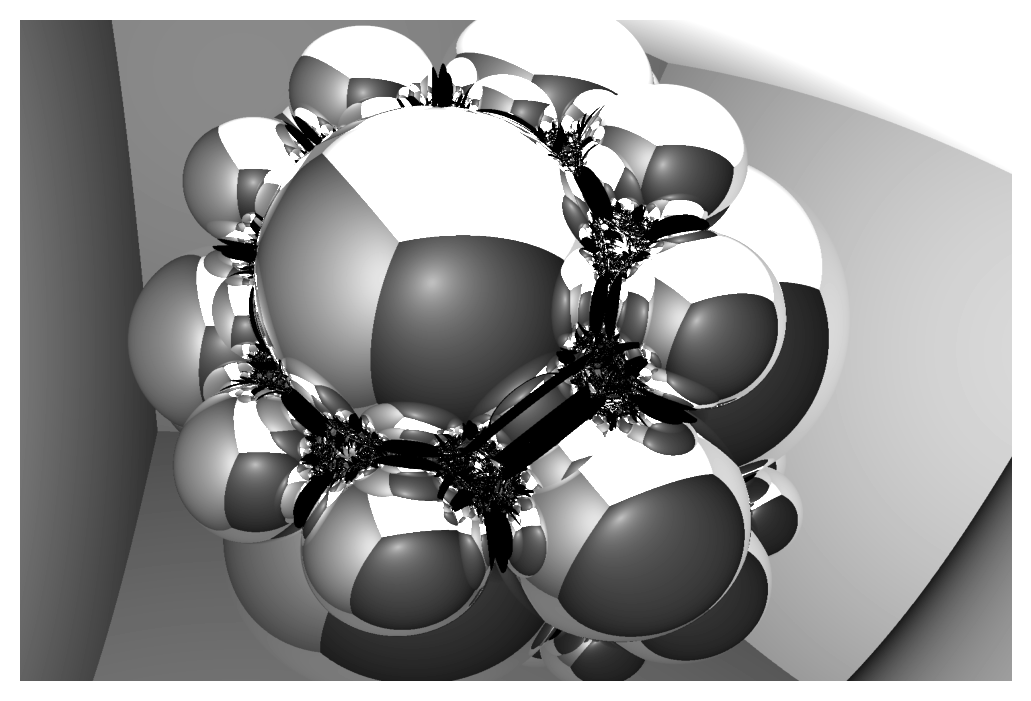
Cool, now we have a weird shiny raspberry
Already these visualizations raise some interesting questions, like
- What is the fractal dimension of this sphere packing?
- Why do I want to bite into these spheres so much?
Higher Generations
While my code allows for GPU use, I’m using my tiny GPU-less laptop, and after generation 2 it starts to complain.
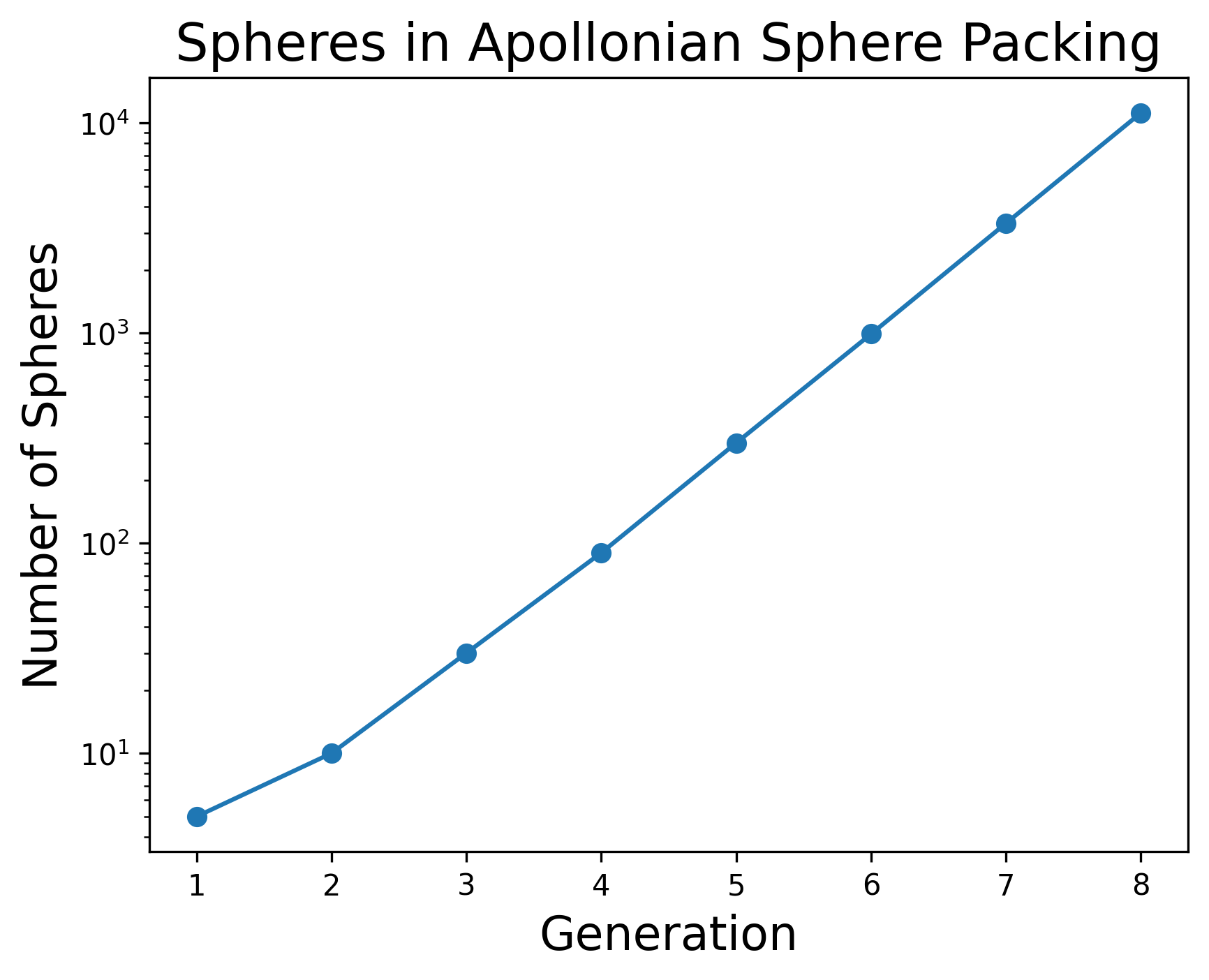
As you increase the generations of this fractal, the number of spheres increases exponentially. Here are the spheres which make up the 6th generation shown by themselves:

(note the dark shadows between nearby spheres).
This kind of sucks, and although it’s certainly possible to plot these sphere packings at high fractal generations, I’m being maximally dumb here – using essentially no tricks to speed things up. Ray tracing is known for being slow, and for our sphere packing, tons of rays just get stuck bouncing around between the collection of spheres – that’s what all the jet black regions between them are.

Let’s try to get a fractal some other way – actually, let’s try to use those annoying dark regions where rays are getting stuck.
Secret Sierpinski
Remember that first generation with the tetrahedron? Well look at the middle – there are three spheres being reflected. Each of those spheres is reflecting its own smaller set of three spheres, etc. This is feeling pretty fractal-y.
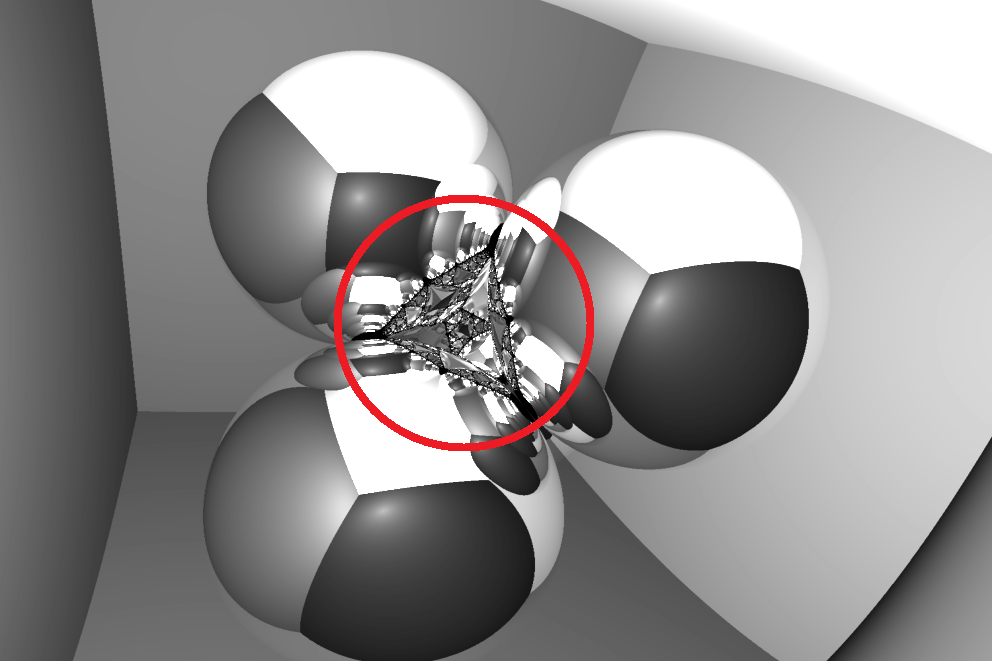
Look between those three spheres. There are some rays that are still bouncing around a few generations, which show up as black. This is clearer if we plot just the rays which haven’t hit a wall yet.

This looks quite a bit like a Sierpinski triangle – and it looks that way because it’s being constructed the same way. Consider how repeated reflections work here. When a bunch of rays go between our four spheres, each sphere reflects them at the three other spheres. This gives us three dark patches in our image. But each of these dark gaps is reflected at three other spheres too, etc. This leads to an iterative construction that exactly matches that of a Sierpinski triangle.

It turns out there’s a close relationship between apollonian gaskets (which our sphere-packing is a 3d version of) and Siepinski triangles – they share the same combinatorial structure. But who cares about that honestly. Let’s just see some pretty pictures

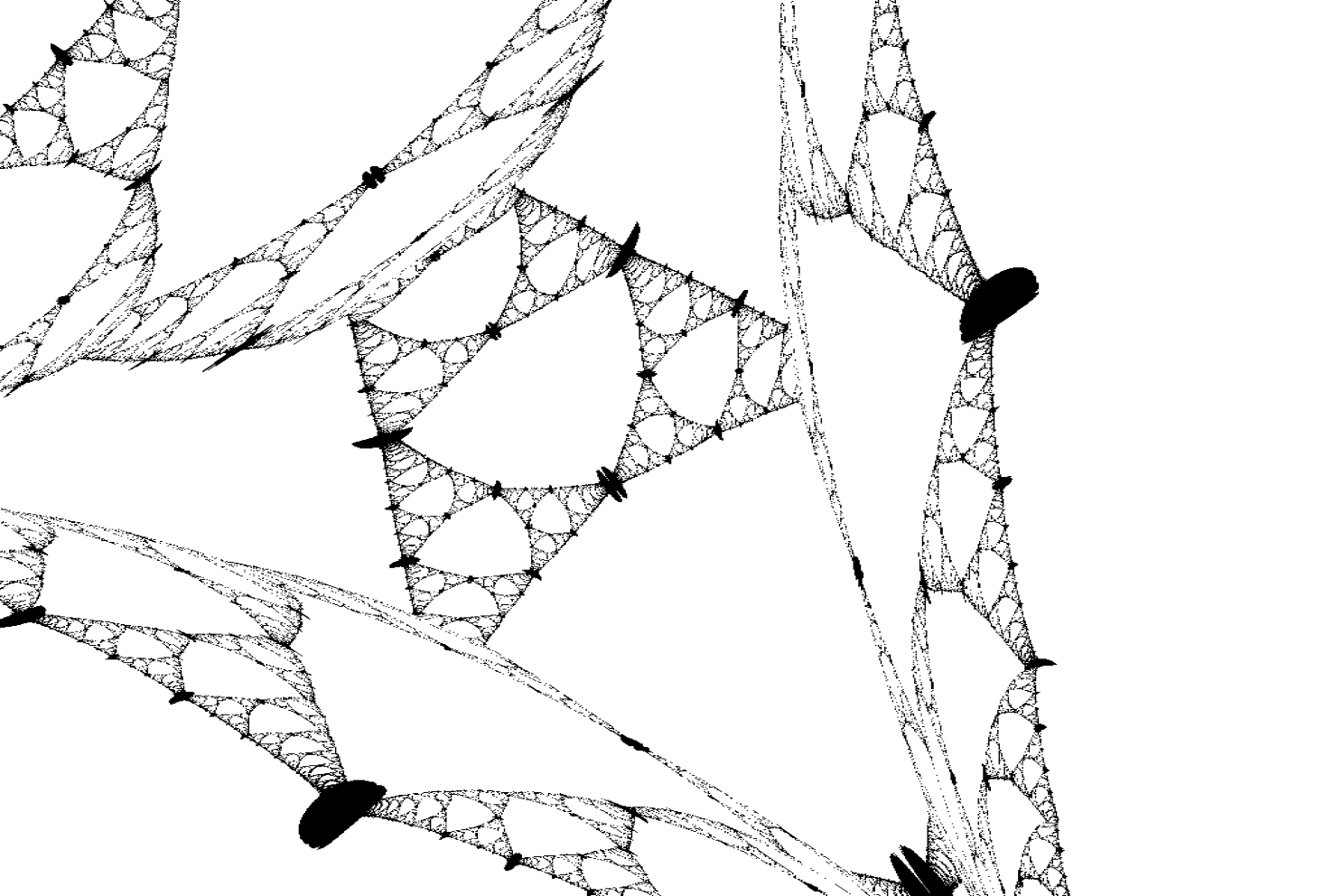
To the left are the full reflection surfaces, and to the right we plot those rays still-reflecting in black.


Conveniently, since this is a fractal, you get the picture at this point. It's all the same, literally.
Fractal Zoom
Now I know what you’re thinking: “does this mean that if I get 4 ball-bearings together, go into a white room, make myself invisible, and use an also-invisible microscope to zoom in between them, I’ll see a fractal??”
I think so, but that whole procedure seems really involved. How about we zoom in with this ray tracer thing and see what happens. (Also, I’ve always wanted to make one of those fractal-zoom videos)
