The first time I ever gambled was in Las Vegas. My friend Chad and I both sat at a slot machine, inserted a dollar bill, and hit the button (apparently, they don’t use levers anymore?). The symbols raced by for a few moments, and when they stopped spinning, we both learned that we had lost a dollar, and our first gambling experience was over.
This experience represents basically all of my interactions with gambling. Volatility doesn’t really do anything for me thrill-wise. In fact, I’ve organized my life largely to minimize volatility.
But suppose a bookie gives odds for some event to occur, and the implicit probabilities from those odds do not add to 1. If this occurs, then I can make money. Importantly, I don’t make money in expectation or something – no, I make money literally whatever happens. The bets I use to make this money are called a Dutch book. I was recently biking through the Netherlands, and, reinforced by the other dutch things around me (the windmills, the canals, the stroopwafels), the concept of a dutch book became lodged in my mind.
The fact that such dutch books could exist explains exactly why even the criminal underbelly has no choice but to use math. (take that, criminal underbelly). If they refused, threatening to give a swirly to the nerd who told them their odds didn’t add up, somebody like me could come by and make a wager that they would take, and that would necessarily cost them all their money.
This equilibrium leads us to the situation in which people must use probabilities to express their intuitive confidence in events. To somebody who uses Bayesian reasoning, this isn’t all that surprising. Cox’s theorem already tells us we should use probability to express our subjective confidence of an event occurring, so what would the alternative be? These types of questions are things that philosophers worry about. Skimming through the dutch book page on the Stanford Encyclopedia of Philosophy, the first hyperlink reads “The Basic Dutch Book Argument for Probabilism”. As soon as you start talking about whatever “probabilism” is, you have lost me.



What is interesting to me is the equilibrium we all implicitly live at, in which every ‘gambler’ is forcing every ‘bookie’ to maintain consistent probabilities. It reminded me of the dynamic of a GAN, in which a discriminator identifies differences between a dataset and a generator’s outputs. During training, these models battle one another; the discriminator finds a flaw in the generator’s outputs, and the generator frantically tries to patch it up. Ideally, the equilibrium of this game should lead to the generator producing samples which ‘look like’ they’re from the distribution of the dataset.
Since I liked this adversarial dynamic so much, I thought I would try to apply the same computational physics to the topic of dutch books. Here’s the idea: we’ll parameterize a bookie (with, let’s say, \(\theta\)) and a gambler (we’ll call these parameters \(\phi\)). As I’ve said, the point of a dutch book is that a gambler can make money whatever happens. Therefore in our setup, the gambler tries to maximize his minimum possible payout. At the same time, we’ll have the bookie try to minimize this minimum possible payout
Conceptually we’ll have something like
\[\dot{\phi} = \alpha \frac{d}{d\phi}\left(\text{Minimum Payout}(\theta, \phi)\right)\] \[\dot{\theta} = -\beta \frac{d}{d\theta}\left(\text{Minimum Payout}(\theta, \phi)\right)\](Where \(\alpha\) and \(\beta\) are the relative learning rates of each)
I should emphasize, I’m not going to take random samples, do actual simulations, or compute expectations – these are just a set of odds that the gambler is trying to manipulate to get free money regardless of what could occur.
If everything works, we should see that the bookie learns to revise their odds in such a way that they’re not always losing money, which should imply that their implied probabilities are positive and add to 1.
Basically, we’re going to force a bookie to discover the basics of probability theory.
Here’s the setup:
Suppose \(N\) horses are in a race, we’ll be concerning ourselves with which horse wins (we’ll set \(N=5\) ).
A bookie is parameterized by the payouts for each horse winning the race. The \(i^{th}\) horse will have odds written \(x_i / 1\)
This means that if I put 1 dollar on this horse winning the race, and it wins, I get \(x_i\) dollars plus the initial investment of 1 dollar. On the other hand, if I put a dollar on this horse losing the race and it loses, I recoup \(1/x_i\) dollars in addition to my investment. Of course, if I’m wrong, I of course lose my money either way.
Let’s parametrize the gambler by a set of \(2 N\) parameters \(\{ w^{(W)}_i, w^{(L)}_i \}\) . This is the wagers ( \(w\) ) they’re putting on the \(i^{th}\) horse winning ( \(w^{(W)}_i\) ) and losing ( \(w^{(L)}_i\) ). In total, if the \(j^{th}\) horse wins, the gambler gets a payout of
\[\text{payout}_j= (x_j w^{(W)}_j - w^{(L)}_j) + \sum_{i\neq j} (w^{(L)}_i/x_i - w^{(W)}_i)\]Now just to keep things finite, let’s fix the total amount of money we allow our gambler to bet. We’ll do this by defining parameters \(\{ z^{(W)}_i, z^{(L)}_i \}\) so that
\[w^{(W)}_i = \frac{\exp(z^{(W)}_i)}{\sum_i \exp(z^{(L)}_i)+\sum_i \exp(z^{(W)}_i)}\] \[w^{(L)}_i = \frac{\exp(z^{(L)}_i)}{\sum_i \exp(z^{(L)}_i)+\sum_i \exp(z^{(W)}_i)}\]Basically every iteration, we give the gambler one dollar to play with. Okay, after initializing the odds according to a log-normal distribution, let’s see what happens.
The Results
First, the minimum winnings of our model:
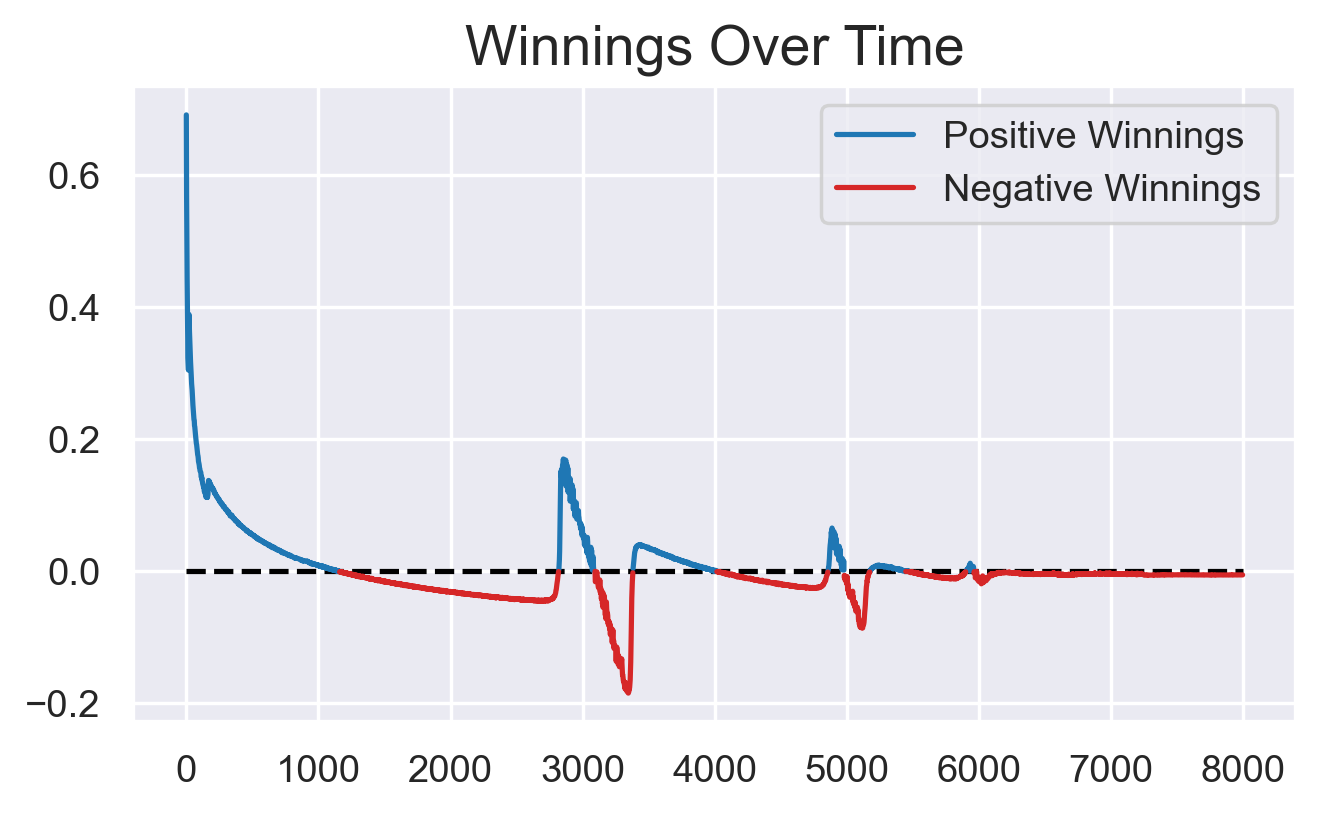
Cool, it seems that our gambler repeatedly discovers bets to make money (in blue), before the bookie catches on and changes the odds. What exactly is going on?
When I look at the bets, it seems they all kind of do the same thing – flipping between betting on all the horses winning and betting on all of them loses. Let’s take a look:
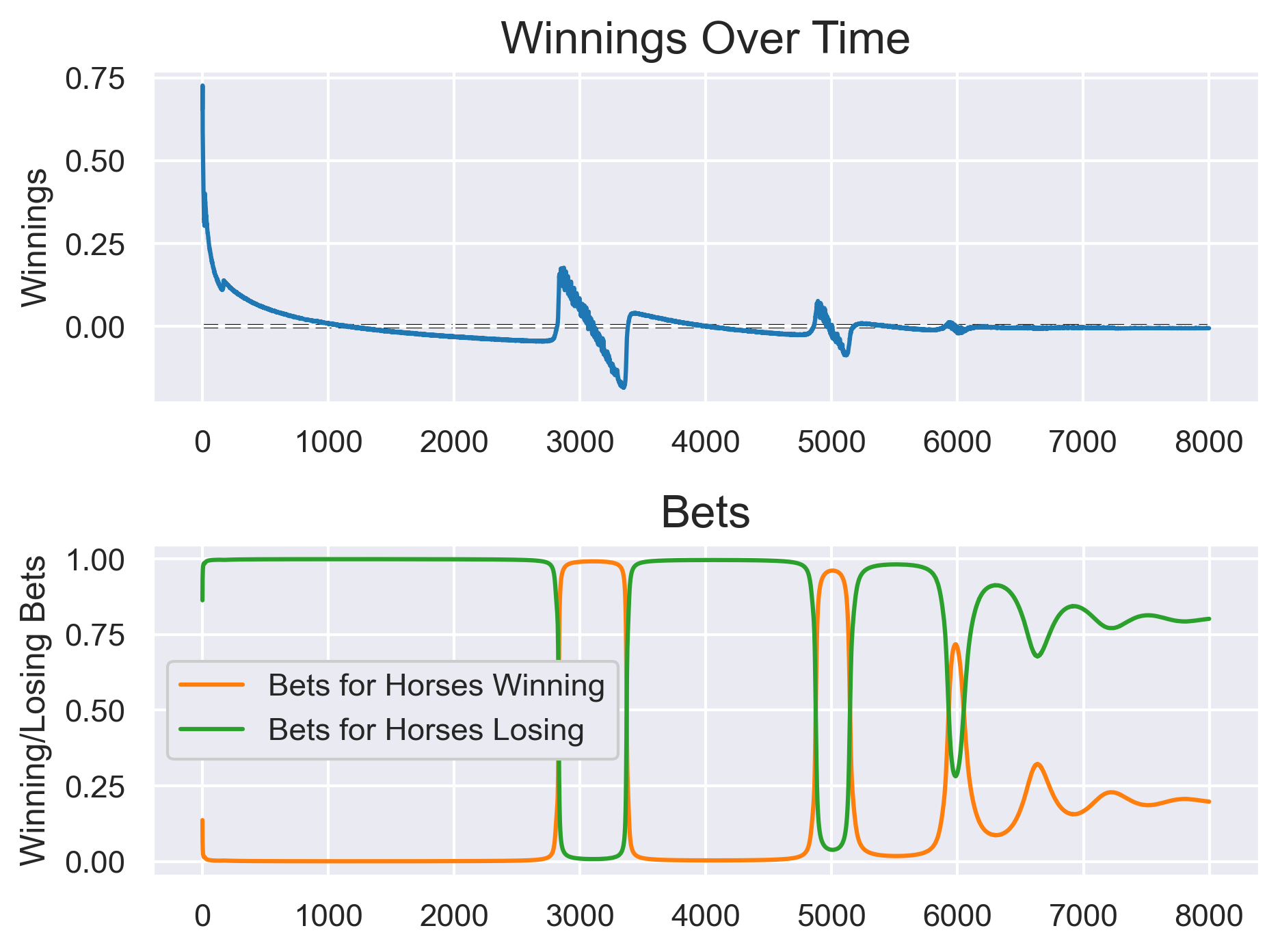
In the smooth descending regions, the gambler is placing bets on every horse to win. Meanwhile, in the steeper regions, the bets have flipped. Now they’re putting all their money on the horses losing. If I were a bookie, and a gambler came up to me and confidently made a wager that every horse would lose, I would probably check my math. Then again, this bookie doesn’t know math.
How can we explain this? Well lets finally look at the sum of implicit probabilities: \(\sum_i (1+x_i)^{-1}\) . Remember, this bookie doesn’t even know what probability is. All they know is that they have these odds \(\{x_i\}\), and that they keep getting screwed out of money.
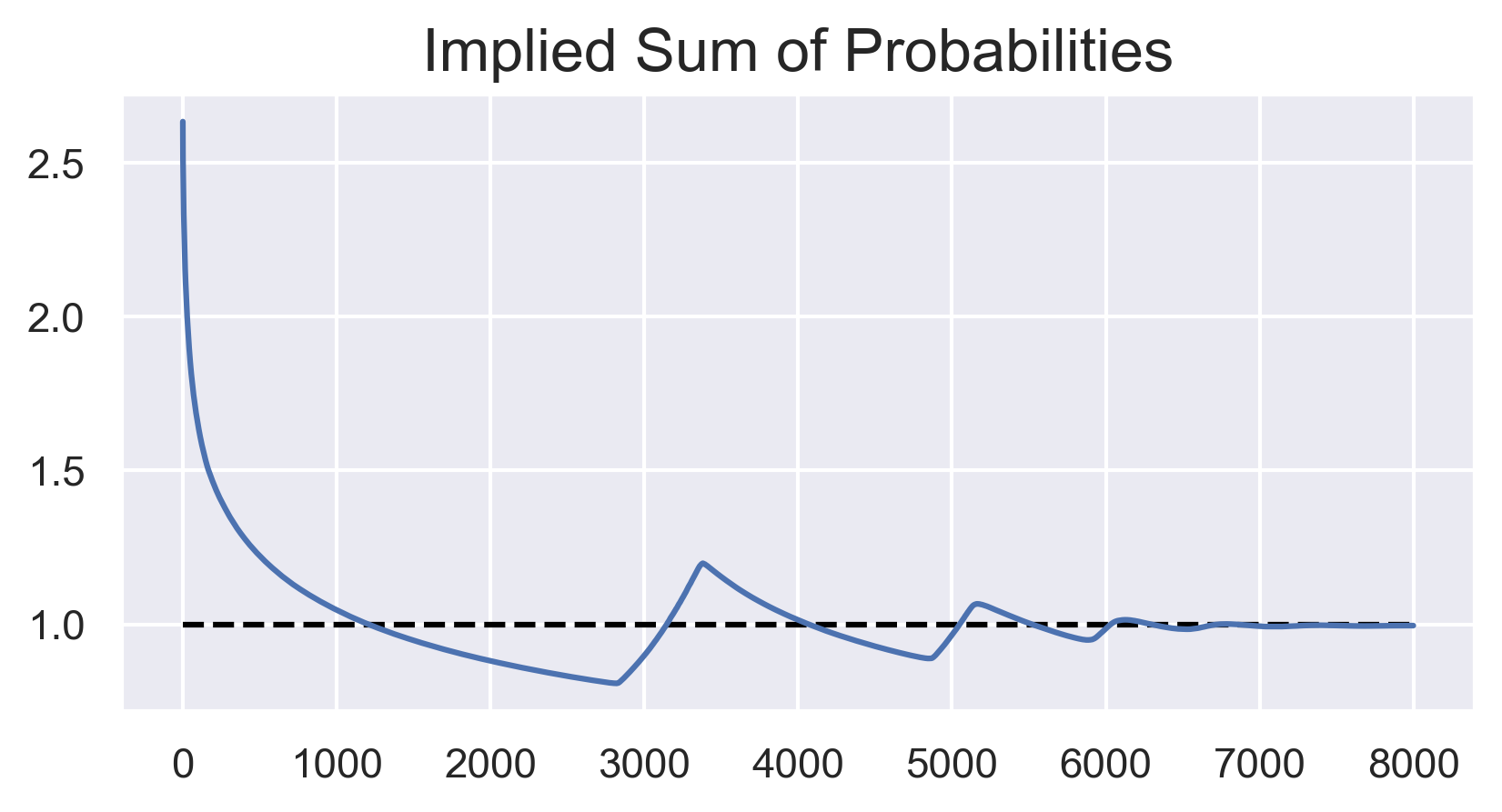
Awesome! Looks like our bookie has learned probability theory! If only they had paid attention in school, we wouldn’t need to do this the hard way. This plot also tells us what’s going on with this repeated pattern we see of a power-law drop in minimum rewards, followed by a linear drop.
At first, the sum of probabilities of each horse winning is greater than 1. This means any horse losing is undervalued, so our savvy gambler bets on everyone losing. The power-law comes from the \(1/x_i\) in the payout function if all bets are on horses losing:
\[\text{payout}_j= - w^{(L)}_j + \sum_{i\neq j} w^{(L)}_i/x_i\]When the probability drops below 1, the event of any horse winning is underrated, so we bet on that. This makes the reward drop linearly, since if we only bet on winning,
\[\text{payout}_j= x_j w^{(W)}_j - \sum_{i\neq j} w^{(W)}_i\]\(x_j\) enters in, and the reward drops linearly. Basically, its just an artifact of how we’ve parameterized the odds.
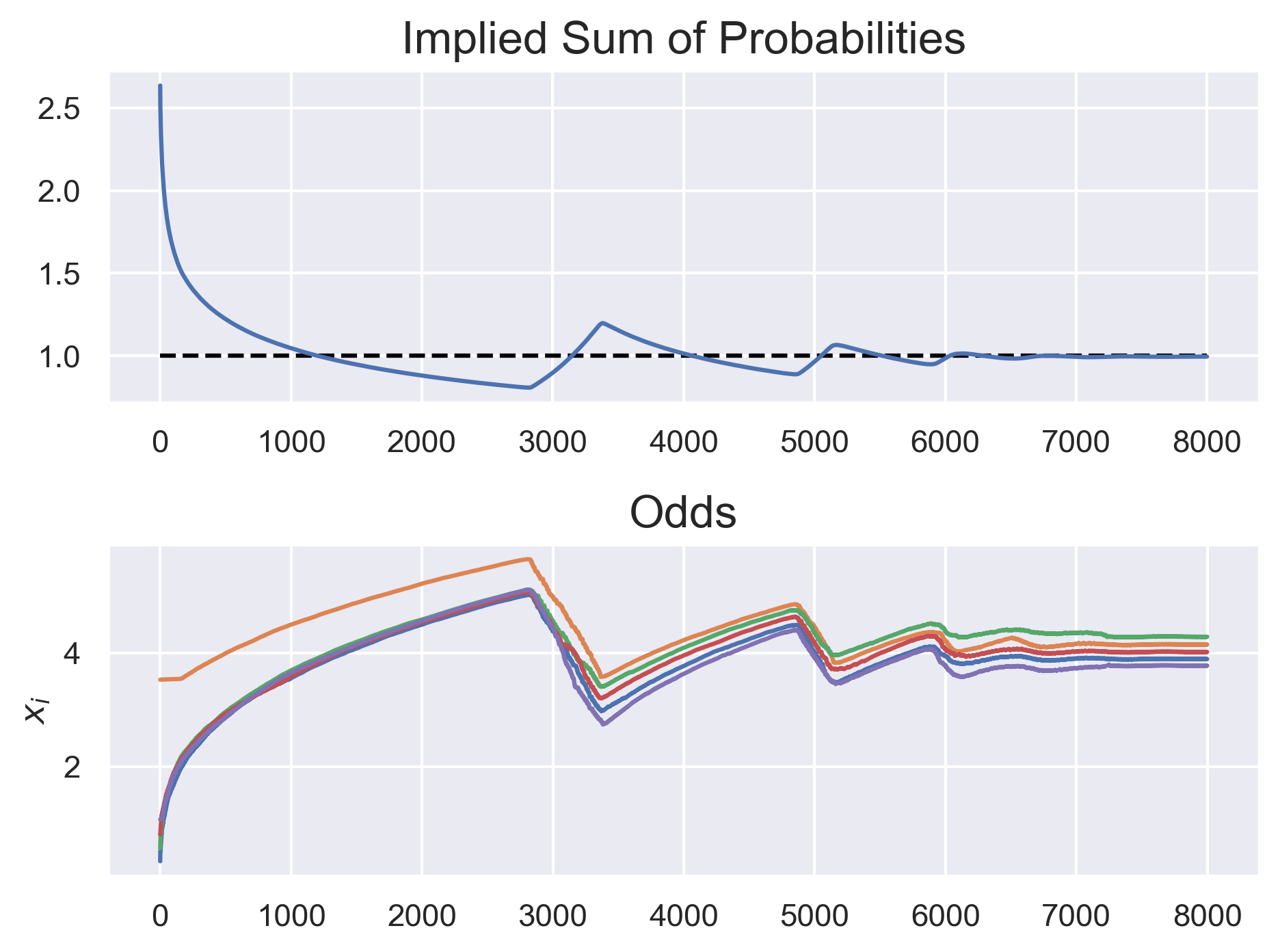
So what’s the point of this? I keep emphasizing that the bookie doesn’t know probability theory, as if we do. But of course, we don’t really know it either – at least not naturally. We use things like the availability heuristic to formulate probabilities. I do like to believe that, just like this bookie, we can get better at setting probabilities.
Maybe we should all investigate some of our beliefs to make sure nobody can scam us either.
