
Something I noticed a while back was that, although in general, people on motorized two-wheeled vehicles (hereafter referred to as MOTORCYCLES) look cool, there are cases when they do not.
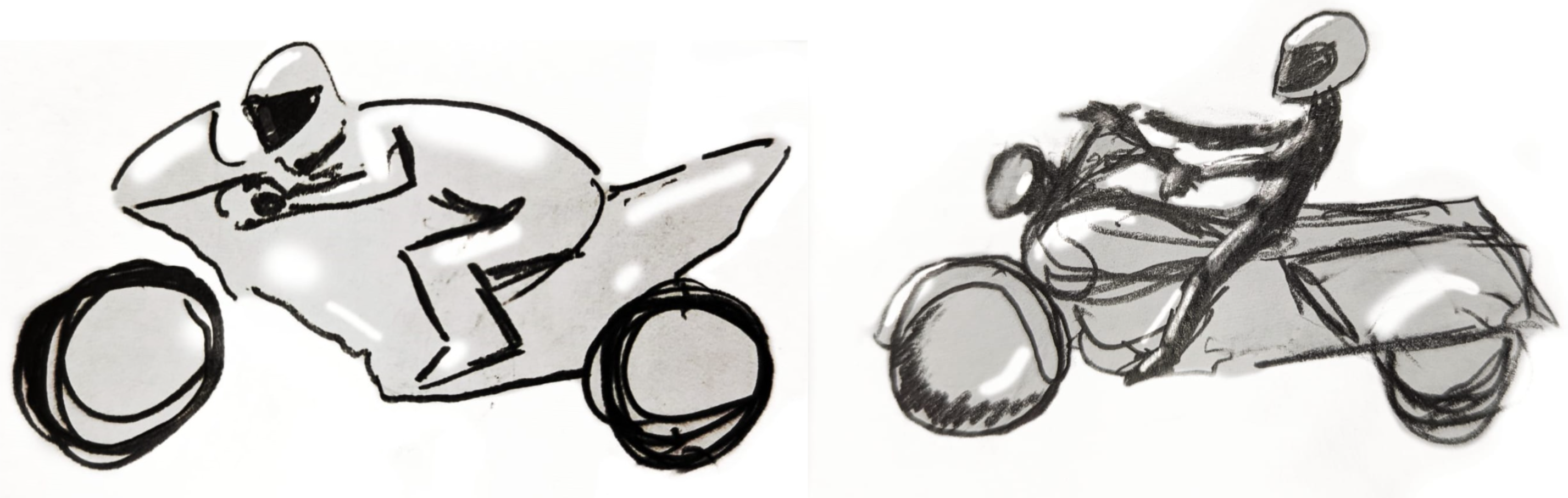
For example, both of these riders look cool:
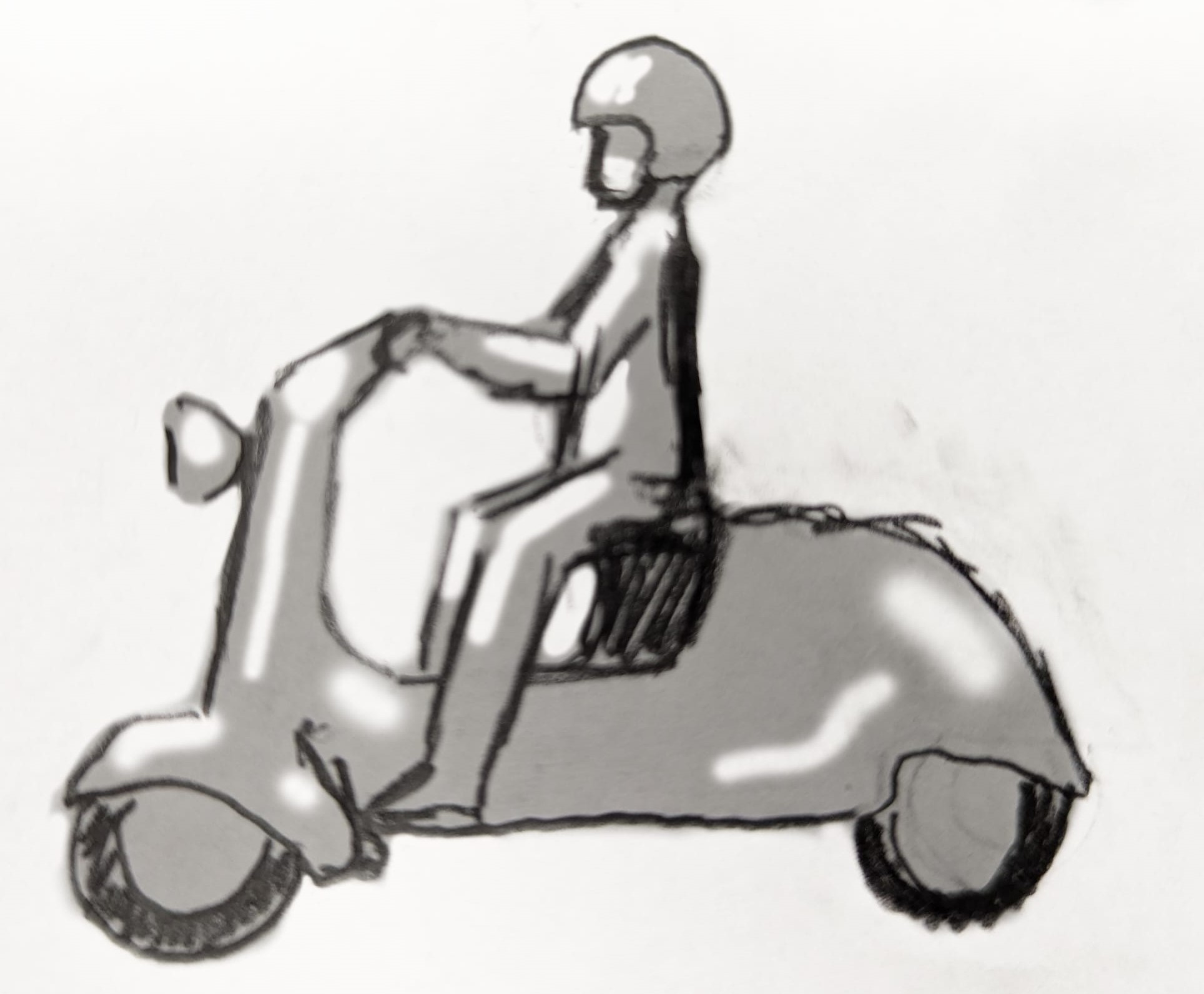
This rider, however, definitely does not look cool.
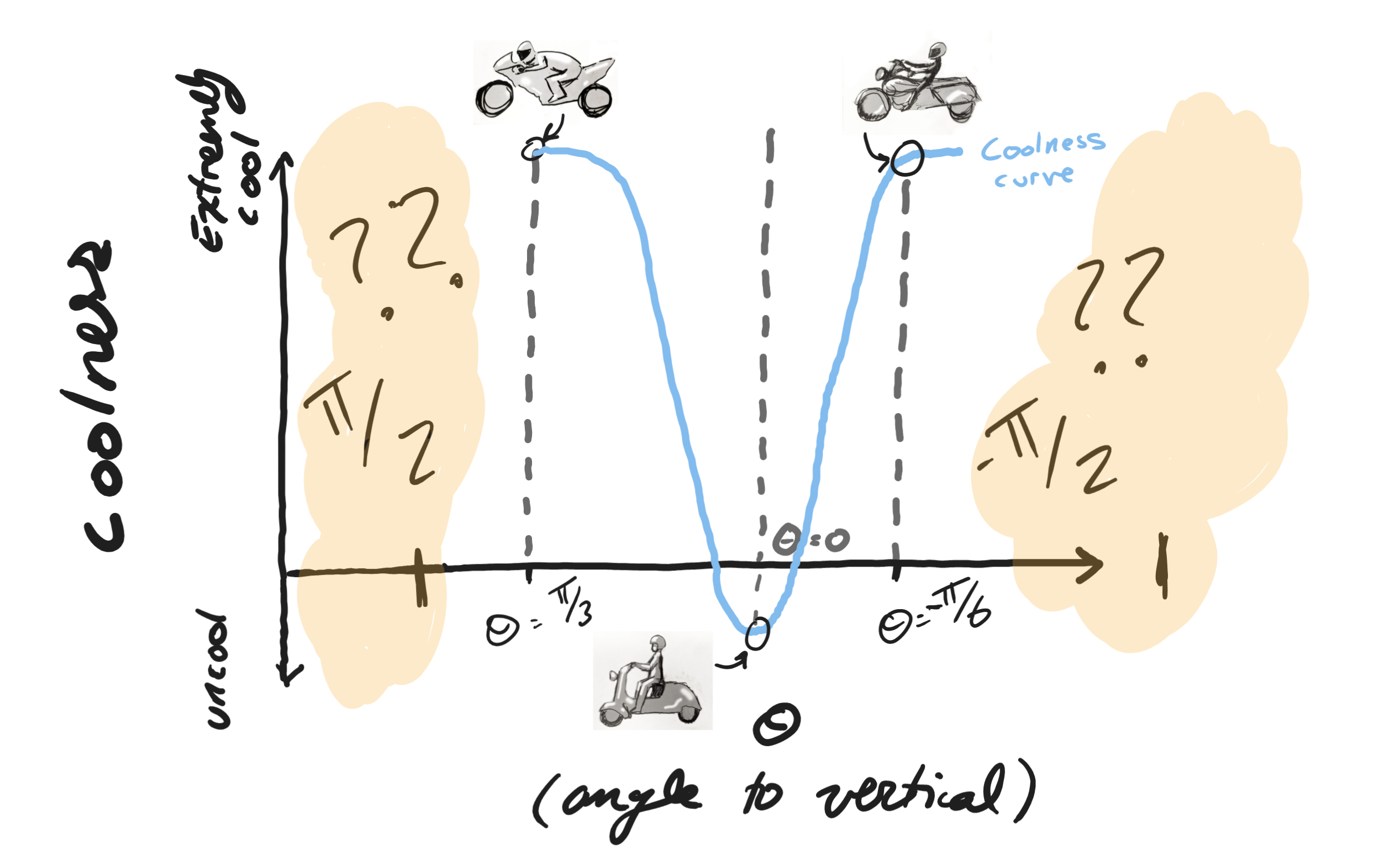
To explain this phenomenon, I have formulated a theory: coolness on a motorcycle is a function of seating angle of the back with respect to the vertical, as shown below:
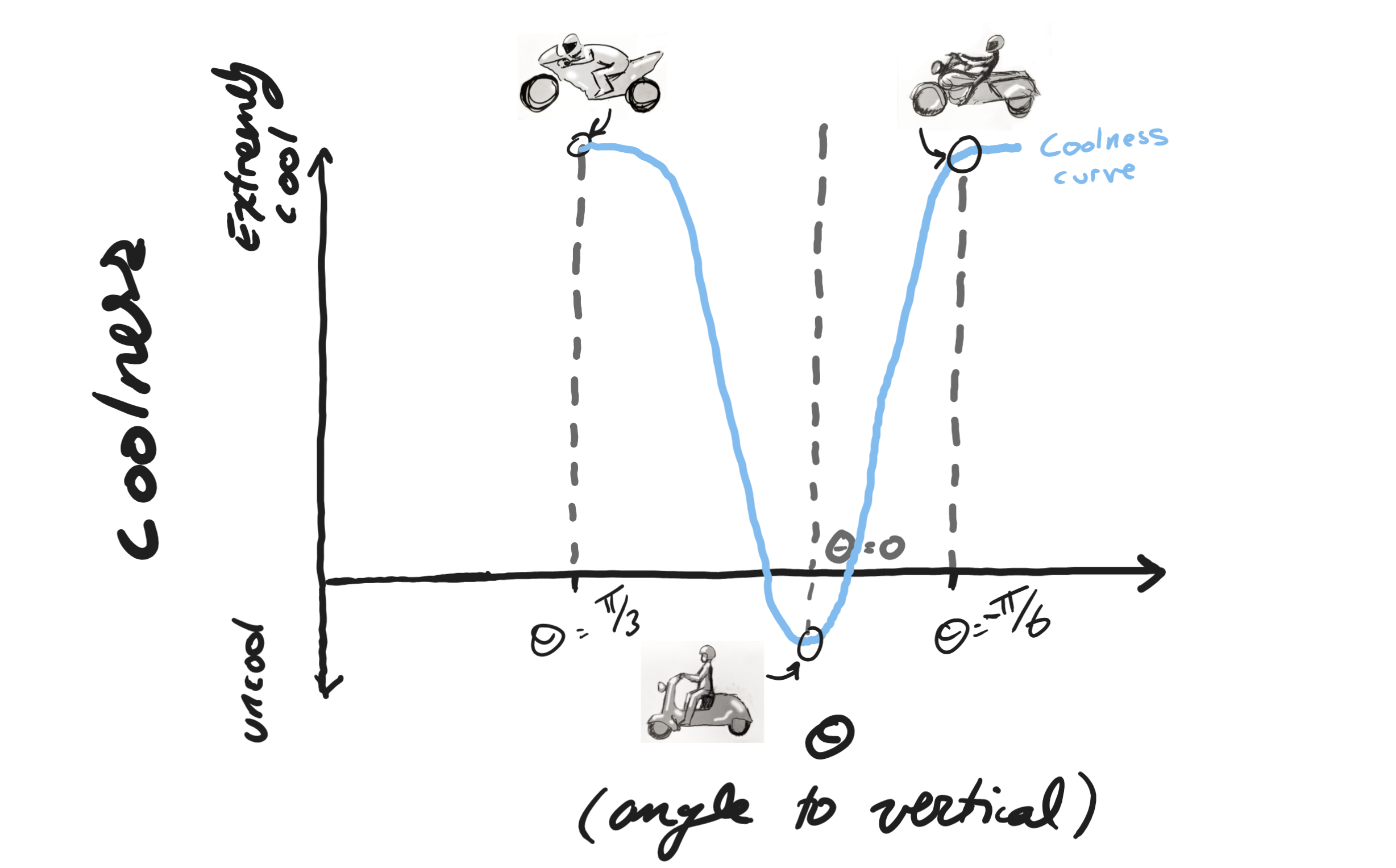
Around $\theta=0$ this obeys the equation
\[\text{Coolness}(\theta) = C_{mop.} + (1-e^{-\left(\frac{\theta}{\pi/10}\right)^2})(C_{sup.} - C_{mop.})\]Where above, $C_{mop.}$ is the coolness of a moped (coolness minimum), and $C_{sup.}$ is roughly the coolness of the superbike (coolness supremum).
To be specific, let’s take a look at the seating angle of the two cool riders. (Leaning backward is considered a negative angle, and leaning forward is considered positive.)
On the superbike, the rider has an angle of roughly $\pi/3$.

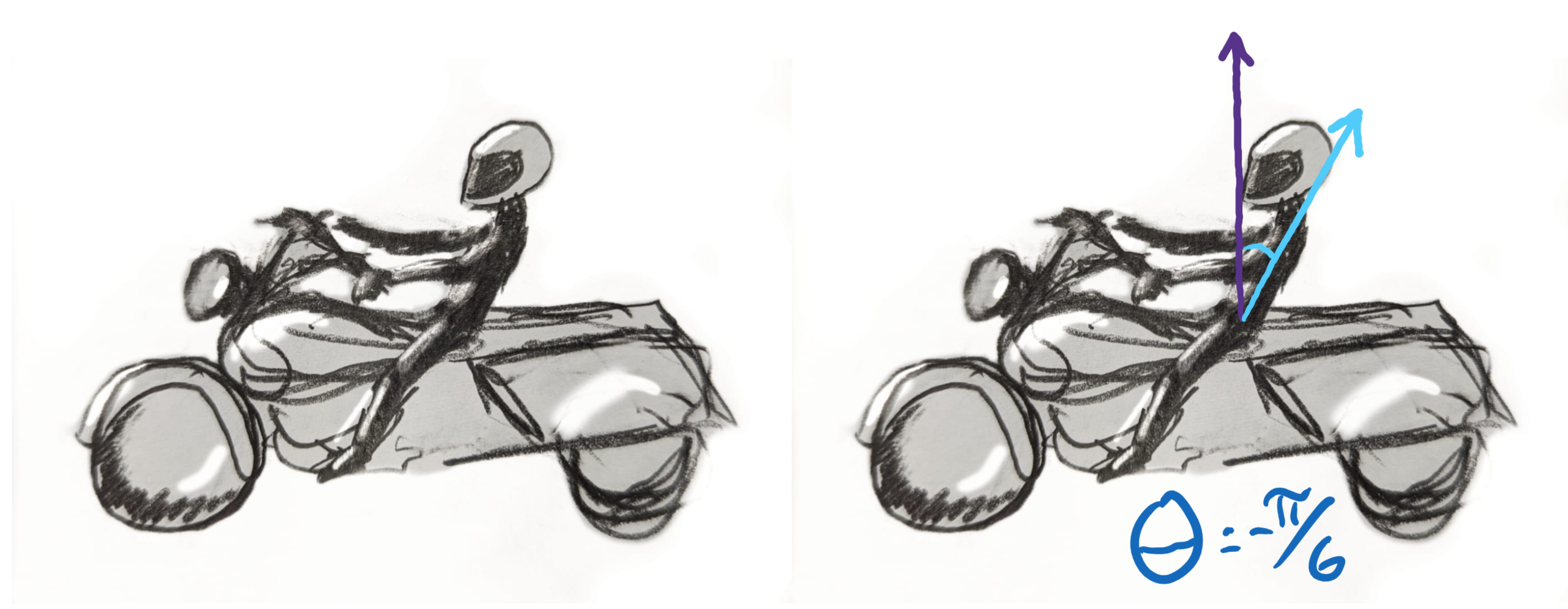
On the harley, the rider has an angle of around $-\pi/6$.
But on the moped the rider has an angle of $0$. This represents the minimum of the coolness vs angle curve.

This makes sense, and clearly we’ve proven this theory is true beyond a doubt — but it also raises some questions (helpfully indicated by the question marks below).
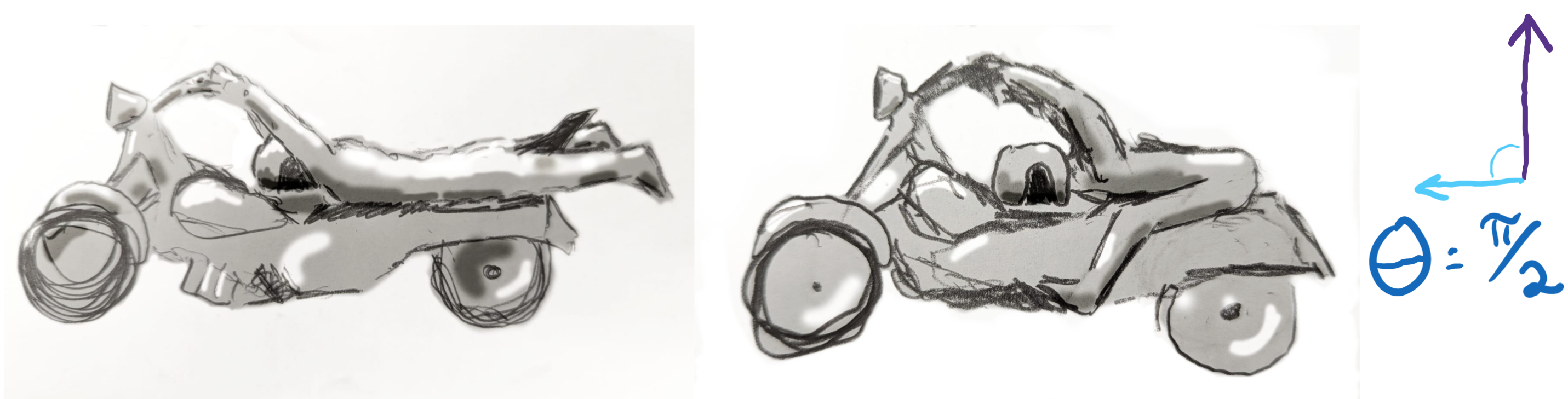
Exotic Motorcycle Riding Configurations
What does my seat-angle theory of motorcycle coolness say about these regimes?
How do we even begin to investigate the coolness of $\theta=\pm \pi/2$. First, we need to ask, how does one ride a motorcycle when sitting at $\theta=\pm\pi/2$?
At these extreme points in seating-angle-space, the orientation of one’s legs might have two distinct positions which are equally good options to the rider – on the footpegs, or off the bike entirely. The orientation that the biker eventually chooses depends on which side of the foot-placement-phase they end up on.

Now we need to try to evaluate the coolness of these configurations. On the one hand, all are extraordinarily dangerous — it is impossible to see what’s in front of you when your face is oriented directly into the seat ($\theta=\pi/2$). Dangerous things are inherently cool, so this works in their favor. On the other hand, these positions also look incredibly stupid, which can be uncool.
These positions represent exotic configurations in motorcycle riding space, and they might only exist in certain extreme environments: like empty bolivian salt flats, or within the interiors of neutron stars. In these regimes, we might observe a breakdown of our parochial understanding of what motorcycling is – let alone how cool a given position is.
Probing these kinds of profound mysteries are exactly what science is about – so please take this poll to help contribute to humanity’s collective understanding of the coolness of motorcycle-riding positions.
Big news everyone – I was recently informed by my Estonian architect friend that one of these exotic phases of motorcycle usage has already been employed in the real world.

He was aptly named “Rollie Free” – and roll free he did, in a speed-o no less. This is science in action. I (a scientist) make a prediction and, like Einstein’s prediction of gravitational lensing being observed during a full solar eclipse, my prediction of the existence of an exotic state of motorcycling is confirmed by examining nature (wikipedia). Rollie even did this this on salt flats (Bonneville Salt Flats) – just as I predicted.
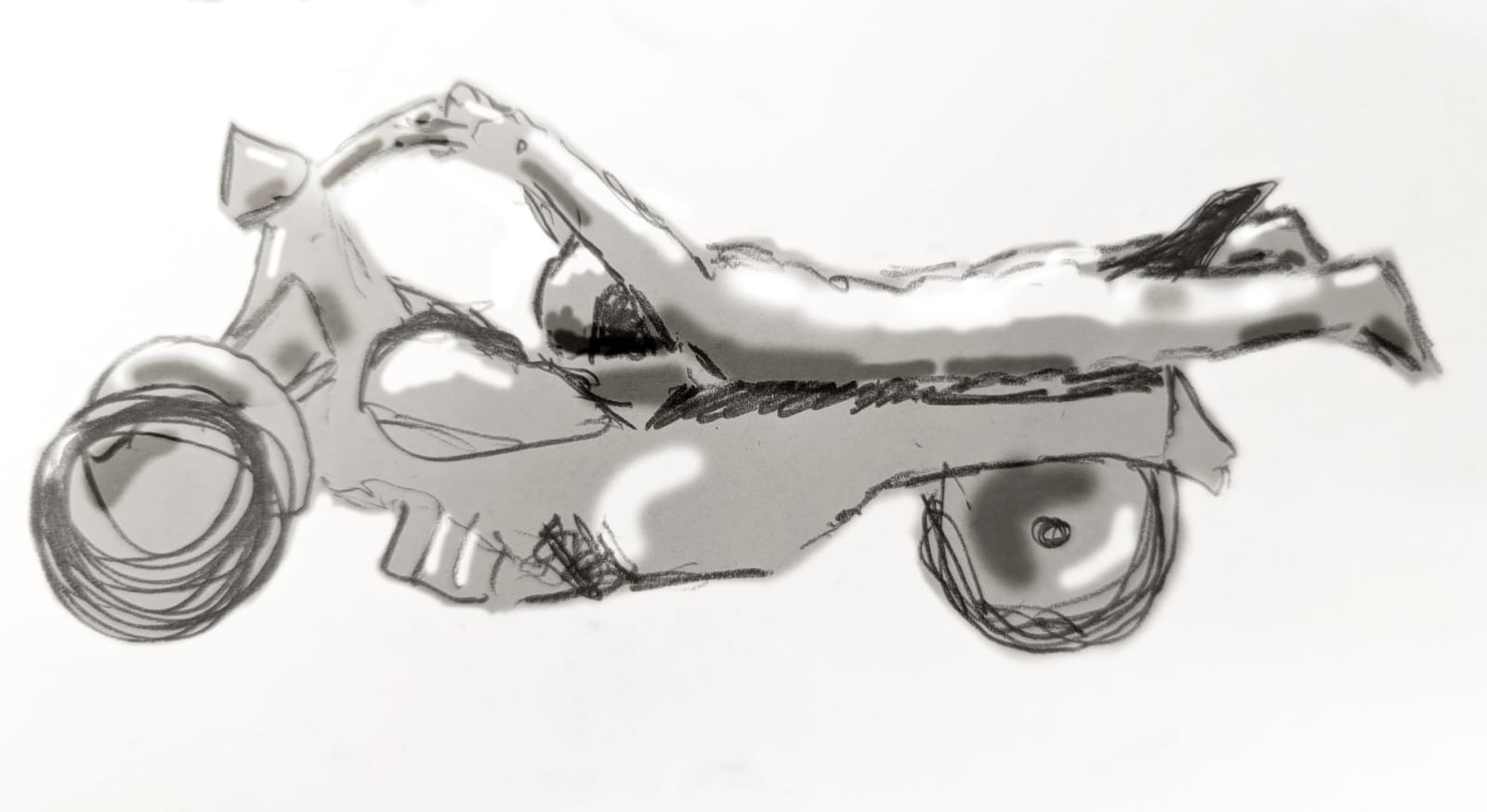

Rollie’s near-nudity reinforces his insane coolness more than theoretical predictions ever could. We now know for sure how one rides a motorcycle when they drive at an angle of $\pi/2$ to vertical, and how profoundly cool they look.

I’ll be sure to keep this blog updated the second I learn of further real-world examples of exotic phases of motorcycle riding, and their corresponding coolnesses.
